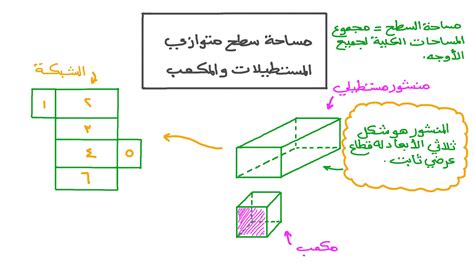
مساحة ضلع متوازي المستطيلات، متوازي المستطيلات هي مادة هندسية صلبة مكونة من 6 أوجه، ولحساب مساحة ضلع متوازي المستطيلات، نحتاج إلى حساب مساحة بعض الوجوه من خلال معرفة الطول. عرض وارتفاع متوازي المستطيلات.
جدول المحتويات
سطح مربع

- نظرًا لأن الأضلاع المتقابلة من المربع متطابقة، يمكننا حساب مساحة المربع فقط من خلال معرفة مساحة 3 جوانب ثم ضرب تلك المساحة في 2.
- يمكن استخدام القانون التالي لإيجاد مساحة متوازي المستطيلات:
- مساحة الصندوق = (الطول × الارتفاع × 2) + (العرض × الارتفاع × 2) + (العرض × الطول × 2).
ولا تنس قراءة مقالنا: مساحة ومحيط متوازي المستطيلات
وجه متوازي المستطيلات

- لذلك عند البحث عن المساحة الجانبية لمكعب متوازي، والتي يمكن حسابها بحساب مساحة متوازي المستطيلات ثم طرح مساحة الجزء العلوي والسفلي من تلك المنطقة، فإن مساحة الجانب هي مساحة 4 جوانب فقط.
- يمكن استخدام القانون التالي لإيجاد وجه الصندوق:
وجه متوازي المستطيلات = (العرض × الارتفاع × 2) + (الطول × الارتفاع × 2).
بعد أن أخذ الارتفاع كعامل مشترك في القانون السابق، يمكن تبسيط القانون إلى:
وجه متوازي المستطيلات = الارتفاع × 2 × (الطول + العرض).
خصائص متوازي المستطيلات

- يتكون الشكل شبه المكعب من 6 أوجه متوازية، وكل وجه من هذه الوجوه عبارة عن مستطيل.
- إذا عرفنا طول متوازي المستطيلات وعرضه وارتفاعه، فيمكننا حساب مساحة سطحه.
- مساحتها الجانبية وكذلك حجمها، حيث أن العديد من الخزانات لها شكل منشور مستطيل، لذلك نحتاج إلى معرفة الحجم لمعرفة كمية السائل المخزن.
- يحتوي الصندوق على 8 زوايا، ويتم تعريف الزاوية على أنها نقطة التقاء 3 حواف للمربع.
- كل زوايا الصندوق هي زوايا قائمة ويمكن حساب حجم الصندوق باستخدام الصيغة التالية:
الحجم = الطول × العرض × الارتفاع.
- المكعب هو حالة خاصة لمكعب يمكن أن يتحول إلى مكعب إذا كانت وجوهه مربعة بدلاً من مستطيلات.
- يُطلق على الخط الذي يفصل بين جانبين متجاورين من المربع اسم حرف، ويتكون المربع من 12 حرفًا.
ولا تتردد في زيارة مقالتنا حول الموضوع: قانون حظر الحجم مع المراجع
المثال الأول لحساب مساحة جانبية متوازي المستطيلات
- في هذا المثال نريد حساب مساحة الصندوق الجانبي إذا كان ارتفاعه 8 سم وطوله 6 سم وعرضه 5 سم.
- إذا طبقنا القانون المفصل أو القانون المبسط لحساب المساحة الجانبية، فسنجد أن المساحة الجانبية تساوي 176 سنتيمترًا مربعًا.
المثال الثاني هو حساب مساحة سطح متوازي المستطيلات

- في هذا المثال نريد حساب مساحة سطح متوازي المستطيلات إذا كان ارتفاعه 8 سم وطوله 6 سم وعرضه 5 سم.
- باستخدام القوانين المذكورة، سنجد أن مساحة سطح متوازي المستطيلات تساوي 236 سنتيمترًا مربعًا.
مثال عملي لحسابات متوازي المستطيلات

- إذا كان هناك مسبح مستطيل يبلغ طوله 20 مترًا وعرضه 15 مترًا وعمقه 4 أمتار، فما تكلفة دهانه عندما يبلغ سعر المتر المربع 20 جنيهًا إسترلينيًا.
- في هذا المثال، نحتاج إلى حساب المساحة الجانبية لخط متوازي السطوح لأننا لن نرسم قاع البركة وبالطبع لن نرسم قمته أيضًا، وباستخدام القوانين سنجد مساحة الجانب تساوي 280 مترا مربعا.
- وإذا قمنا بضرب المساحة الجانبية في تكلفة اللوحة لكل متر مربع، نحصل على تكلفة اللوحة التي ستصل إلى 5600 جنيه إسترليني.
اقرأ أيضًا: شكل متوازي المستطيلات في الرياضيات
وهكذا، من خلال موقع تريندات، تعلمنا طريقة حساب المساحة الجانبية للمكعب، وكذلك حساب مساحة سطحه وحجمه، وذكرنا خصائص متوازي المستطيلات قبل النظر في أمثلة عملية على الفوائد من هذه القوانين.