بحث عن الإحداثيات القطبية والمركبة

بحث عن الإحداثيات القطبية والمركبة، يحتاج الكثيرون إلى إجراء بحث عن إحداثيات قطبية ومركبة، والإحداثيات هي أرقام تصف الموقع النسبي.

أوجد الإحداثيات القطبية والمركبة

قد يحتاج الكثير من الناس إلى البحث عن الإحداثيات القطبية والمركبة التي يحتاجونها في حياتهم العلمية وكل بحث يحتاج إلى العديد من العناصر لتوضيح ما يلي:

1- الإحداثيات القطبية

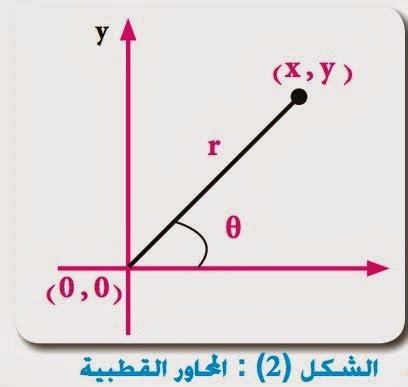
• نظام الإحداثيات القطبية هو نظام إحداثيات ثنائي الأبعاد يحدد موقع كل نقطة داخل المستوى، ضمن المسافة التي تفصل كل نقطة عن المركز وفي زاوية بين الخط المار عبر المركز والنقطة نفسها.
• نظام الإحداثيات هو مجموعة من المتغيرات التي يمكن من خلالها معرفة موضع نقطة داخل مستوى ثنائي الأبعاد.
• يوجد نظام إحداثيات ديكارتي يستخدم نظام الإحداثيات الكروية أو القطبية ونصف القطر وزاوية الإسقاط داخل الدائرة الاستوائية وزاوية الإسقاط على الدائرة القطبية الشمالية.
• نظام الإحداثيات القطبية هذا بسيط لأنه يعبر عن العلاقة من خلال نقطتين من حيث المسافة والزاوية، تمامًا كما هو الحال في البندول.

2- أنواع الإحداثيات القطبية

1- إحداثيات أسطوانية

• إنه أحد الأنظمة ثلاثية الأبعاد التي من خلالها يمثل نقطة في ثلاثة رموز وهي p و g و q. يرمز إلى بعض المصطلحات الديكارتية التي تعني نصف القطر.
• الإحداثيات الأسطوانية هي المسافة بين المحور y والنقطة الموجودة داخل المستوى.
• الإحداثي هو الزاوية بين المحور والنقطة m داخل المستوى x و y
• المسافة لها علامة سالبة وتقع في منتصف المستوى x و y والنقطة m.

ولا تنس قراءة مقالنا: تحليل الفرق بين مربعين في الرياضيات بالأمثلة

2- الإحداثيات الكروية

• إنه نظام إحداثيات قطبي ثلاثي الأبعاد يتكون من نصف قطر، وسمت، وسمت، وأوج.

3- إحداثيات دائرية

إنه نظام إحداثيات ثلاثي الأبعاد يعبر عن النقطة م بدلالة n، t، l.

نظام إحداثيات ثلاثي الأبعاد

• يعمل على توفير الأبعاد المادية الثلاثة: الطول والعرض والارتفاع، ويأخذ نظام القياس شكل x و y و g.
• يمكننا اشتقاق إحداثيات النقاط x و y و g بالأبعاد على المستوى y و g وكذلك المستوي x و y. يمكن تقسيم النظام ثلاثي الأبعاد إلى 8 مناطق وهي مناطق نصف ثنائية الأبعاد.

أنا أيضًا أدعوك لتعلم: إيجاد المتجهات في مستوى الإحداثيات

أنظمة الإحداثيات الرئيسية ونظام الإحداثيات القطبية

أولاً، نظام الإحداثيات الديكارتية

• يعتمد هذا النظام على تحديد موقع نقطة برقمين يسميان إحداثي س وإحداثي ص، والمعروفين باسم الخط المتدرج، وتُعرف الإحداثيات باسم التفاصيل والموقع.
• أولاً، نقوم بإسقاط عمودين، المحور السيني والمحور الصادي، ويجب توحيد وحدة الطول والتدرج بشكل موحد داخل القطاع.
• من خلال النظام الديكارتي، من الممكن تحديد الأشكال الهندسية، على سبيل المثال دائرة نصف قطرها يساوي 2، ويمكننا التعبير عنها بالمعادلة س تربيع + ص تربيع = 4.
• تمت تسمية النظام الديكارتي على اسم عالم الرياضيات رينيه ديكارت، وهو علم بذل جهدًا كبيرًا في الجمع بين الجبر والهندسة.

ثانياً، نظام الإحداثيات البيضاوي

• إنه نظام إحداثيات ثنائي الأبعاد حيث تكون الإحداثيات بيضاوية الشكل ومحدودة داخل التركيز.

ثالثًا، نظام الإحداثيات الأسطواني

• إنه نظام إحداثيات ثلاثي الأبعاد يتم فيه تحديد نقاط الفضاء بواسطة حدثين قطبيين، وهما الطائرات الثابتة والمسافة التي يتعين القيام بها وإسقاطاتها المتوازية على بعض
• من خلال المستويات والإحداثيات القطبية الأولى، يطلق عليها المسافة الشعاعية أو نصف القطر.
• أما بالنسبة للإحداثيات القطبية الثانية فيشار إليها بالموقع الزاوي أو زاوية السمت أما بالنسبة للإحداثيات القطبية الثالثة فيمكن بالطبع أن تزيد إذا كان المستوى المرجعي أفقيًا.
• يُطلق على الخط العمودي الذي يمر عبر المستوى المرجعي المحور الطويل أو محور الأسطوانة، ويمكن أن يمتد هذا الخط من النقطة المركزية للإحداثيات.
• يمكن استخدام نظام الإحداثيات الأسطواني عند التعامل مع الأشياء أو الظواهر ذات التناظر الدوراني حول المحور الطولي.
• يمكن استخدامه أثناء تدفق المياه في أنبوب مستقيم ذو مقطع دائري.

رابعًا، نظام الإحداثيات الكروية

• إنه نظام إحداثيات ثلاثي الأبعاد يمكن من خلاله تحديد موضع النقطة بثلاثة أرقام.
• موضع النقاط هو زاوية ارتفاع أو ارتفاع النقطة من المستوى الثابت عبر نقطة الأصل والمسافة الإشعاعية المقاسة من نقطة ثابتة تسمى نقطة الأصل.
• زاوية السمت هي النقطة الثالثة التي تقع بين الإسقاط المتوازي للخط الذي يربط بين النقطة والأصل داخل مستوى ثابت واتجاه ثابت داخل نفس المستوى.

اقرأ هنا عن: قائمة أعظم علماء الرياضيات والفيزياء

تحديد إحداثيات معقدة

• الأعداد المركبة هي أحد أسس الرياضيات وتتكون من رقمين مركبين وهما رقم أساسي والرقم الثاني هو الرقم المركب ويسمى العدد التخيلي للأعداد المركبة.
• تستخدم الأعداد المركبة في مختلف العلوم، ليس فقط في الرياضيات، وخاصة في الجبر. تُستخدم الأرقام المركبة في جميع أنواع الإلكترونيات والكهرباء والديناميكيات.
• الإحداثي المركب هو الحل النهائي لمعادلة رياضية تشبه صور بعض الأرقام، بما في ذلك X ^ 2 + a ^ 2 = 0، حيث يكون الرمز a رقمًا حقيقيًا ولأنه رقم حقيقي، تتم كتابة المعادلة على هذا النحو س ^ 2 = -a ^ 2.
• أخيرًا نقول إن العدد المركب هو أي رقم يمكننا كتابته بالصورة p = a + b c.

الأعداد المعقدة والعمليات المعقدة

• نظرًا لأن العنصر A والعنصر B عبارة عن أرقام حقيقية والعنصر T هو جذر تربيعي لسالب واحد، فإن العنصر A وحده هو رقم مركب حقيقي والعنصر B هو جزء تخيلي من رقم مركب.
• يمكننا التعبير عن أي مجموعة من الأعداد المركبة بالرمز k بالمعادلة التالية: k = n، z = a + bv، لأن a – b ينتمي إلى l – t = ¬ root of -1.
• أولاً، يتم التعبير عن عملية الإضافة في العمليات المعقدة بالمعادلة التالية: h1 = a + bv – w 2 = c + dc.
• يمكننا التعبير عنها بالعلاقة التالية (أ + ج) + (ب + د) تي}، لذلك يجب أن يؤخذ في الاعتبار أن أي إضافة إلى الأرقام المعقدة التعسفية هي عملية مضافة ومغلقة، وهي أيضًا عملية تبادلية .
• يتم دمج الأرقام المركبة أثناء عملية الجمع بين المعكوس الجمعي والعنصر المحايد.
• ثانيًا، في العمليات المعقدة، يتم إنشاء عملية الطرح بالمعادلة التالية {h1 = a + bt and h2 = c + dt}.

التمثيل البياني ضمن الأعداد المركبة

• أولاً، يمكن كتابة العدد المركب في أي رسم بياني بطريقة، هذه الطريقة هي a + b، ويمكنها تعيين زوج مرتب من الأرقام الحقيقية.
• يمكننا تمثيل الرقم (أ، ب) بنقطة على المستوى الديكارتي أو داخل المتجه الرئيسي بحيث يبدأ من الأصل وينتهي بالنقطة التي إحداثياتها أ، ب.
• تسمى الأرقام المركبة بالإحداثيات الديكارتية أو مستوى أرجاند، ويعود هذا الاسم إلى العالم الفرنسي أرغوند، ويسمى المحور الرأسي المحور التخيلي ويسمى المحور الأفقي بالمحور الحقيقي.

في نهاية المقال، تعرفنا على العناصر التي ستساعد في كتابة بحث عن الإحداثيات القطبية والإحداثيات المعقدة، وأنظمة الإحداثيات القطبية والمعقدة، وأنواع الإحداثيات القطبية، والأرقام المركبة، ورسم الأرقام المركبة مع تعريف الإحداثيات المعقدة. .