حل السؤال لكل زاويتين متقابلتين في متوازي أضلاع

أهلا وسهلا بكم زوار تريندات. في قطاع التعليم، نقدم لك خدمة للإجابة على أسئلتك التعليمية والحياتية في جميع المجالات. تريندات يتعامل في المقام الأول مع الجانب التربوي ويتيح للطلاب من جميع المستويات الإجابة على جميع أسئلتهم التعليمية

أي زاويتين متقابلتين في متوازي الأضلاع؟، وبما أن متوازي الأضلاع هو شكل هندسي ثنائي الأبعاد، فإنه يتميز بوجود أربعة جوانب فقط، وفي هذا المقال سنتحدث بالتفصيل عن متوازي الأضلاع وسنشرحها جميعًا. الخصائص التي تميز متوازي الأضلاع عن الأشكال الهندسية الأخرى.

ما هو متوازي الاضلاع؟

متوازي الأضلاع هو مربع بسيط لا يتقاطع داخليًا وله زوجان من الأضلاع المتوازية بداخله، لأن متوازي الأضلاع له أربعة أضلاع، لذا فإن كل ضلع متقابل متوازي ومتساوي الطول، ومتوازي أضلاع له أربع زوايا، ومجموع الزوايا الداخلية لمتوازي الأضلاع 360 درجة، وفي الحقيقة هناك العديد من أنواع وأشكال متوازي الأضلاع، ولكل نوع من هذه الأنواع خصائص تميزها عن الأنواع الأخرى، وفيما يلي أشهر أنواع متوازي الأضلاع وهي:[1]

متوازي الأضلاع المنتظم: هو نوع من متوازي الأضلاع وله أربعة أضلاع بحيث تكون الأضلاع المتقابلة متوازية ومتساوية الطول، وله أيضًا أربع زوايا داخلية مجموعها 360 درجة.
المربع: هو نوع من متوازي الأضلاع له أربعة جوانب متساوية الطول وأربع زوايا داخلية قائمة 90 درجة وأقطارها متساوية في الطول ومتعامدة مع بعضها البعض.
المستطيل: هو نوع من متوازي الأضلاع حيث له أربعة جوانب وكل ضلعين متقابلين لهما نفس الطول والمتوازي، والمستطيل به أربع زوايا داخلية قائمة تساوي 90 درجة وأقطارها متساوية في الطول ومتطابقة.
المعين المعين: نوع خاص من متوازي الأضلاع فيه أربعة جوانب متساوية الطول، وزاوية داخلية قائمة 90 درجة، وأقطارها متماثلة ومتعامدة، لكن الماس ليس له قاعدة موازية للخط الأفقي.

أنظر أيضا: قانون مساحة متوازي الأضلاع

كل الزاويتين المتقابلتين في متوازي أضلاع

الزاويتان المتقابلتان في متوازي الأضلاع متطابقتان تمامًا، وفيما يلي الخصائص الرئيسية لمتوازي الأضلاع التي تميزه عن الأشكال الهندسية الأخرى، وهذه الخصائص هي كما يلي:[2]

أضلاع متوازي الأضلاع متطابقة.
الزوايا المتقابلة في متوازي الأضلاع متطابقة.
مجموع الزوايا المتتالية في متوازي الأضلاع 180 درجة.
إذا كانت أي من الزوايا في متوازي الأضلاع صحيحة، فإن كل الزوايا صحيحة.
تتقاطع أقطار متوازي الأضلاع.
يقسم كل قطري من متوازي الأضلاع الشكل إلى نسختين متطابقتين.
مساحة متوازي الأضلاع هي ضعف مساحة المثلث ذي الضلعين والقطر.
تتقاطع أقطار متوازي الأضلاع عند نقطة تشكل المركز المتماثل لمتوازي الأضلاع، وتسمى مركز متوازي الأضلاع.
مجموع مربعات أطوال الأضلاع يساوي مجموع مربعات أطوال القطر.
مجموع الزوايا الداخلية لمتوازي الأضلاع هو 360 درجة.
متوازي الأضلاع له تناظر دوراني من الدرجة الثانية.
مجموع الزوايا الخارجية لمتوازي أضلاع يساوي مجموع الزوايا الداخلية لأنها رءوس متقابلة.
مساحة متوازي الأضلاع تساوي حجم متجه حاصل ضرب ضلعين متجاورين.

مساحة متوازي الأضلاع

يمكن حساب مساحة متوازي الأضلاع بالصيغ الرياضية التي تقارن تلك المساحة بأطوال الأضلاع الأربعة، والزوايا الداخلية لمتوازي الأضلاع، أو حتى أطوال أقطار الشكل. :

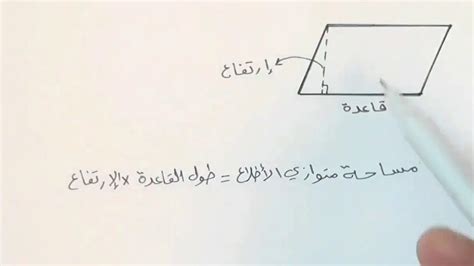
احسب مساحة متوازي الأضلاع من القاعدة والارتفاع

حيث تكون الصيغة الرياضية لهذا القانون كما يلي:

مساحة متوازي الأضلاع = طول القاعدة × الارتفاع

على سبيل المثال، لحساب مساحة متوازي الأضلاع بقاعدته 3 أمتار وارتفاعه 2 متر، يكون الحل كالتالي:

مساحة متوازي الأضلاع = طول القاعدة × الارتفاع مساحة متوازي الأضلاع = 3 × 2 مساحة متوازي الأضلاع = 6 م²

احسب مساحة متوازي الأضلاع من أطوال الأضلاع والزاوية المحصورة

حيث تكون الصيغة الرياضية لهذا القانون كما يلي:

مساحة متوازي الأضلاع = الطول الأساسي × طول الضلع × جيب الزاوية المضمنة

على سبيل المثال، لحساب مساحة متوازي الأضلاع بطول قاعدته 3.5 م والجانب الثاني 1.5 م ومدى الزوايا المضمنة 60 درجة، يكون الحل كما يلي:

مساحة متوازي الأضلاع = الطول الأساسي x طول الضلع x جيب الزاوية المغلقة مساحة متوازي الأضلاع = 3.5 x 1.5 x Sin 60 من متوازي الأضلاع = 4.54 m²

انظر أيضًا: ما هي معادلة مساحة المستطيل؟

في ختام هذا المقال، علمنا أن أي زاويتين متقابلتين في متوازي الأضلاع متطابقتان تمامًا، وشرحنا نظرة عامة مفصلة عن متوازي الأضلاع، وذكرنا جميع خصائص هذه الأشكال الهندسية، وذكرنا القوانين المستخدمة في حساب مساحة متوازي الأضلاع.

العلامات: جوانب، زاويتان، في، كل واحدة، متقابلة، متوازية